In recent years, the precision of MEMS gyroscope has been greatly improved, and has reached the requirements of underground exploration, navigation and aerospace, precision measurement and other fields. It also has a series of advantages that other sensors do not have, such as low cost, miniaturization, high reliability, and easy mass production, and has gradually become the preferred inertial device in the military field and civilian field. In this paper, the systematic error and calibration method of MEMS gyro are analyzed. The systematic error, least square ellipsoid fitting calibration and ellipsoid fitting calibration experiments of MEMS gyro are introduced.
System error of MEMS gyro
MEMS gyroscope used in the inertial system in this paper is composed of three single-axis sensors representing transverse roller axis, pitch axis and heading axis. It can measure the projected component of the angular velocity vector on the three axes. The errors of each single axis gyro measurement mainly include zero position drift, static sensitivity error, random drift error and so on. It is also impossible to achieve complete pairwise orthogonal between the three axes of MEMS gyro, that is, there is a sensitivity mismatch and non-orthogonal error. The error model of MEMS three-axis gyroscope was established as follows:
K=M(Km-K0)
In the formula, Km represents the actual measured value of the gyroscope,K represents the true value, and K0 represents the zero bias error of the gyroscope.
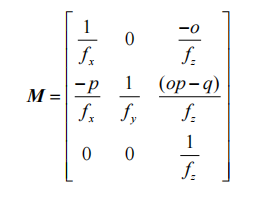
In the formula, ƒx, ƒy, ƒz are the sensitivity of MEMS three-axis gyroscope, and the unit is LSB/g, o,p,q are the Angle between the x, y, and z axes of MEMS gyroscope projected on the XOZ,XOY,YOZ plane and the x axis, y axis and z axis respectively, and the unit is (°). Under ideal circumstances, o,p, and q are 0. The error calibration model of MEMS gyroscopes can be obtained by calculating M and K0 from the above formula.
Least square ellipsoid fitting calibration
The common calibration method for MEMS gyroscope is to use a high-precision rotary table and adopt a full range of positions for calibration, which has great limitations. In this paper, an ellipsoid fitting calibration method which does not require special experimental conditions, is convenient for calibration at the work site, and is fast and accurate for calibration. In an ideal state, the data collected by MEMS gyroscopes will be evenly distributed on a standard sphere, and the actual situation will be affected by its own and external factors, resulting in distribution on an ellipsoid. Ellipsoidal fitting method was used to calibrate the error and construct the ellipsoidal equation. The general quadric equation can be expressed as:
F(M,A)=ax2+by2+cz2+2exz+2dxy+2fyz+...+2px+2qy+2rz+o=0
Where M=[a,b,c,d,e,f,p,q,r,o]T represents parameter vector of quadric surface; μ = [x2, y2, z2, 2xy, 2xz, 2yz, 2x, 2y, 2z, 1] T for the combination of operation under test vector, F (M, μ) as the measurement data (x, y, z) to quadric F (M, A) = 0 algebraic distance, minimum value is the sum of squares:
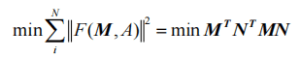
The above formula is used as the judgment criterion for least squares fitting, where:
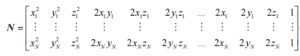
By introducing the ellipsoid constraint condition (X-X0)TC(X-X0)=1, the coefficient matrix can be obtained as follows:
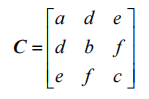
The estimated values of each parameter are as follows:

In the formula, o,p,q represent the non-orthogonal angle in the three-axis gyroscope.
Ellipsoid fitting calibration experiment
Based on the ellipsoid fitting method proposed above, the systematic error calibration of MEMS gyros is carried out. The inertial instrument used in this experiment is HG-4930 MEMS micro-attitude meter, which contains a three-axis MEMS gyroscope. It is output through a digital serial interface bus, and the data communication serial line is RS232. It is powered by a + 5V single power supply. The rotary table used in the experiment is Jiujiang precision three-axis high-precision rotary table. The construction of the experimental platform is shown in Figure 1.

Figure 1 Schematic diagram of gyro fitting experiment platform
The attitude meter used in the experiment is placed on the high-precision three-axis turntable in the laboratory. Firstly, the attitude meter is powered up and preheated for 10 minutes to ensure that all the data of the MEMS gyros are in normal state, the IMU temperature is stable at about 35℃, and the initial position is set as zero. The specific operation steps are as follows:
1. Turn the X-axis of the attitude instrument upward, control the turntable to rotate at a constant speed of 10°/s, and ensure that the turntable rotates 360°. During the rotation process, the upper computer synchronously collects the original data output by the gyroscope;
2. Control the three-axis turntable to adjust the -X axis to face up, keep the speed of the turntable at 10°/s, ensure that the turntable turns 360°, and the upper computer synchronously collects data;
3. Control the three-axis turntable to make the X axis, -Y axis, Z axis and -Z axis face up respectively, and ensure that the rotation speed, rotation range and collection method are exactly the same as the previous two steps.
The above steps ensure that the data contains various gestures, so that the obtained data is better distributed on the ellipsoid, and the calibration accuracy is improved. The collected data were sorted out and fitted with Matlab software, as shown in Figure 2.
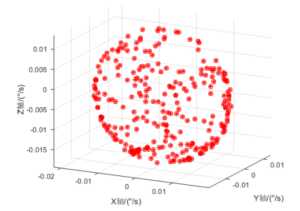
Figure 2 Original data distribution of MEMS gyro
As can be seen from Figure 2, the original data collected is fitted to an ellipsoid shape and on the ellipsoid surface, which indicates the availability of the collected data. Then, according to the above algorithm formula, the center of the three axes of the ellipsoid can be obtained as [-0.0081,-0.0240,-0.0290]. The semi-axis length is [0.1614, 0.1650, 0.1629]. According to the algorithm and derivation in the paper, the error coefficient matrix of the gyroscope can be obtained as follows:

The surface of the fitting ellipsoid is drawn from the above data, as shown in Figure 3(a). Then, the distribution of the original data is drawn together with the fitting ellipsoid for comparison. As shown in Figure 3(b), after fitting the original data, most of the original data are distributed on the sphere of the fitting ellipsoid, which proves that the error coefficient of the fitting ellipsoid obtained from the original output data and the ellipsoid model constructed are practical.
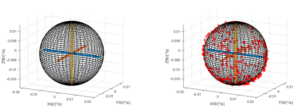
(a) Data fitting ellipso (b) data ellipsoid distribution after fitting
Figure 3 Ellipsoid of MEMS gyro raw data and fitted data
In order to further verify the improvement of output accuracy of MEMS gyroscope by ellipsoidal fitting calibration, 7 groups of positions were selected as the initial positions of the turntable at an interval of 15° between 0° and 90°, and the MEMS gyro sensor was placed on the turntable. The original output data were taken successively, and then the collected original data were brought into the ellipsoidal fitting model for calibration to obtain the output. Compare the two, as shown in Table 1.
| Turntable position angle/° | Uncalibrated angular output/° | Ellipsoid fitting angular output after calibration/° |
| 0 | 1.0944 | 0.0312 |
| 15 | 16.3952 | 14.9840 |
| 30 | 31.2553 | 30.0035 |
| 45 | 46.3976 | 45.0378 |
| 60 | 61.4772 | 60.0465 |
| 75 | 76.5307 | 74.9886 |
| 90 | 91.7156 | 89.9953 |
Table 1 Comparison of angular output before and after compensation
According to Table 1, the uncalibrated angular output and the calibrated angular output after ellipsoid fitting are compared with the Angle of the turntable position to make Angle errors. The comparison results are shown in Figure 4.
As can be seen from Table 1 and Figure 4, the longer the acquisition time, the greater the value of the uncalibrated angle error of the MEMS gyros, and the offset value and scaling factor of the MEMS gyros have changed to some extent. After calibration by ellipsoidal fitting, the data became much more stable, and the maximum measurement error was reduced from 1.7156° to 0.0047°, a reduction of about 2-3 orders of magnitude. It is proved that the ellipsoidal fitting calibration has obvious effect on reducing the system error of MEMS gyros, and reduces the measurement error of MEMS gyroscope with the passage of time.
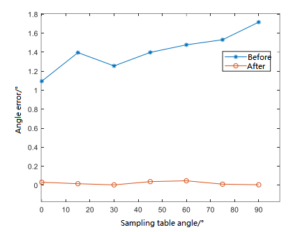
Figure 4 Comparison before and after calibration
Conclusion
The above analysis of MEMS gyro system error and calibration mode, let us have a deeper understanding of MEMS gyro. There are many factors causing the error, such as their own factors and environmental factors, so it is necessary to compensate for the error through calibration. Ericco, as a research and development and manufacturer of MEMS gyroscopes, has a wealth of experimental results and calibration experience, aiming to produce high-performance navigation and tactical MEMS gyroscopes. The ER-MG2-300/400 is a navigation-grade MEMS gyro sensor with a measuring range of up to ±400°/s and a bias instability of 0.03-0.05°deg/hr and an angular random walk of 0.01-0.025°/√hr. The ER-MG-067, as a high-performance tactical MEMS gyroscope, can also achieve the level of bias instability <0.3°/hr and angle random walk <0.125°/√hr.
I hope that through this article, you can understand the knowledge of MEMS gyro. If you are interested in learning more about MEMS gyroscopes, please click on the related products and articles below to learn.
More Technical Questions
1.Sensitive structure analysis of MEMS gyroscope
2.The impact of turntable error on MEMS gyroscope calibration
3.Comparative analysis of typical high performance MEMS gyroscopes
4.The analysis of damping in MEMS gyroscope
5.Wafer-level vacuum packaging of MEMS gyroscope chips
6.Noise Analysis and Solutions of MEMS Gyroscope
Products in Article







