Methods to Maintain the Long-Term Performance of Quartz Flexure Accelerometers

In the field of inertial navigation and inertial guidance systems, accelerometers are one of the core sensing components. They are primarily used to measure the linear acceleration acting on their sensitive axis, providing the instrument with motion velocity and displacement coordinates.

Therefore, the technological level of accelerometers directly determines the technological level of the control system. Among accelerometers, quartz flexible accelerometers have the characteristics of small size, high precision, and high reliability, making them the most mature accelerometers currently available.

This article starts from the structural mechanism of sensors, based on theoretical mathematical models, and proposes relevant improvements in materials enhancement, high-precision machining technology, high-accuracy testing environment.

1.Mechanism of Quartz Flexure Accelerometers

1.1 Basic Structure of Accelerometers

The main structure of quartz flexible pendulum accelerometers is shown in Figure 1. The accelerometer consists of upper torque components, pendulum components, lower torque components, compensating rings, housing, and servo circuits. The upper and lower torque components are composed of magnetic steel, magnetic pole pieces, and compensating rings, while the pendulum component consists of pendulum pieces and upper and lower movable coils.

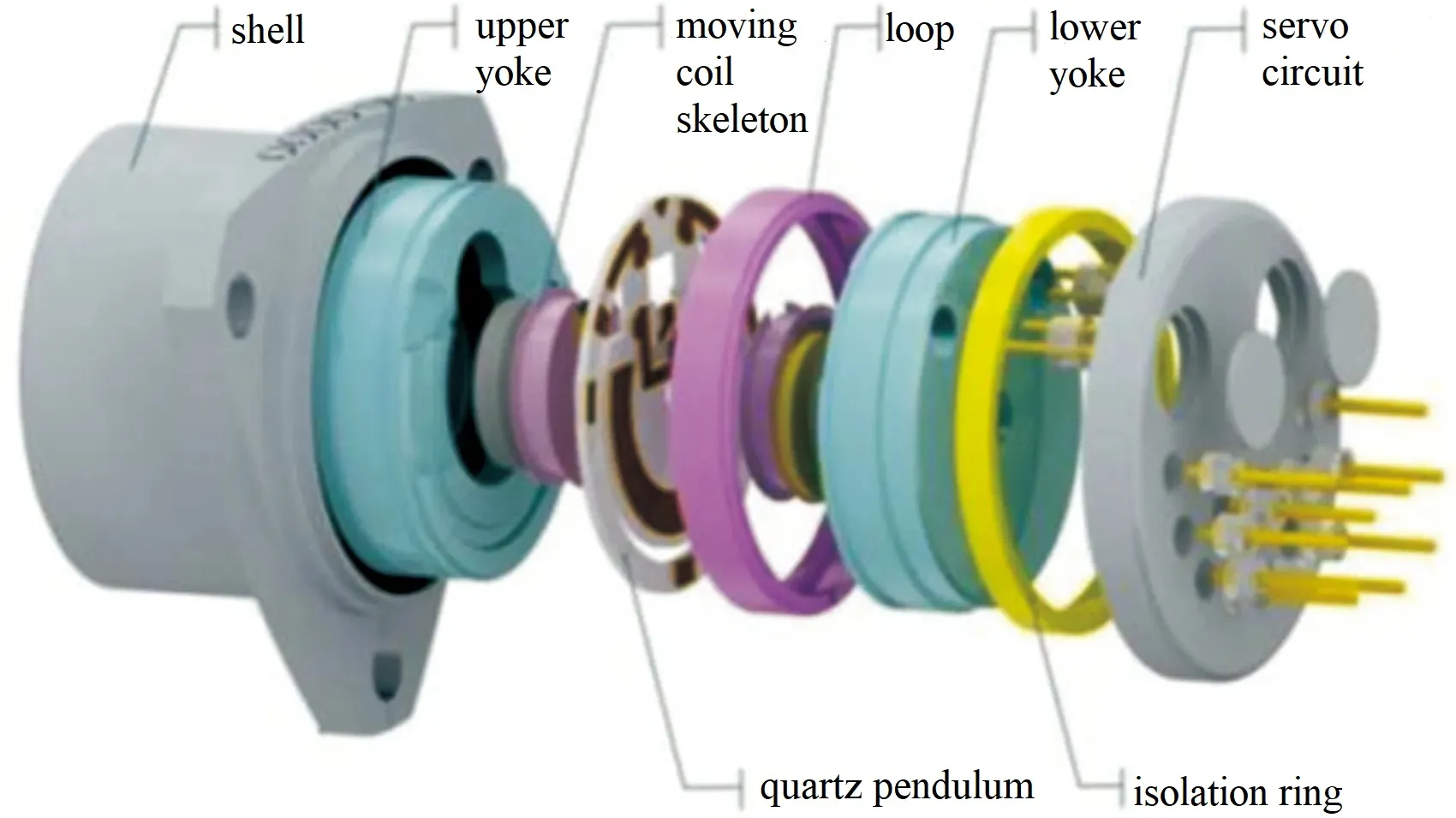
Fig.1 Internal Structure Of Quartz Flexible Accelerometer

1.2 Working Principle of Accelerometers

The pendulum tongue of the pendulum piece and a pair of torque coil bonded to it constitute the detection mass pendulum of the accelerometer. When there is acceleration input along the accelerometer's input axis, the detection mass pendulum will undergo a deflection motion away from the equilibrium position due to inertial effects around the flexible pivot. The differential capacitance sensor on the accelerometer outputs a differential capacitance, which the differential capacitance detector converts into a certain amount of current value. This current is then processed through an integral amplification circuit to form a balanced torque current.

The torque coil is in a stable magnetic field generated by magnetic steel. When a balanced torque current passes through the coil, electromagnetic force acts on the detection mass pendulum to form a balanced torque. The magnitude of the balanced torque is equal and opposite to the inertial torque, allowing the detection mass pendulum to achieve dynamic balance under the action of the balanced torque, completing the detection loop. Refer to Figure 2 for a schematic diagram of the working principle.

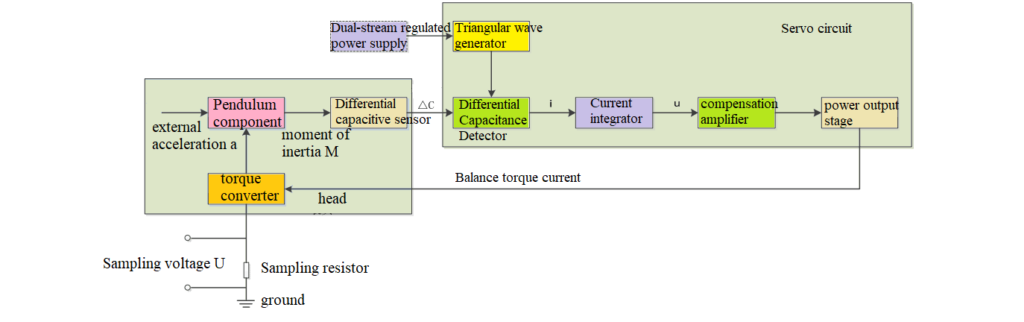
2.Several Paths to Maintain Long-Term Performance of Quartz Flexure Accelerometers

2.1 Mathematical Models

Starting from the structure of quartz flexure accelerometers, based on the theoretical mathematical models of sensors, and utilizing techniques such as mathematical modeling, numerical analysis, model verification, and data mining, improvements are proposed from various aspects such as material enhancement, high-precision machining technology, and high-accuracy testing environment.

This fundamentally addresses the issue of active optimization, guiding production with mathematical models, and predicting the static and dynamic performance of products based on various structural parameters.

2.1.1 Static Mathematical Model

Quartz flexible accelerometers generate error torques around their output axes, resulting in nonlinearity and cross-coupling effects in the performance of accelerometers. To analyze the specific factors affecting accelerometer performance, the following error model is established:

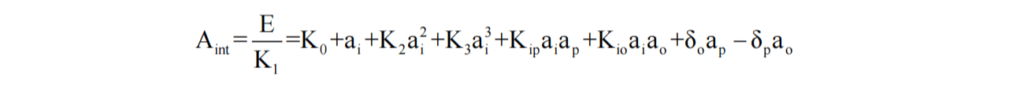
error model

From the formula, it can be inferred that the main causes affecting accelerometer measurement error are: the nonlinear error and stability error of scale factor K1; cross-coupling error caused by offset angle during pendulum component movement; offset error caused by interference torque Md, elastic restoring torque Kh β, and other reasons.

2.1.2 Dynamic Mathematical Model

Refer to Figure 3 for a schematic diagram of the accelerometer pendulum assembly. To analyze the motion characteristics of accelerometers, the movement of the pendulum component under acceleration can be simplified into a bending beam model, based on which a linear kinematic model of the accelerometer can be established:

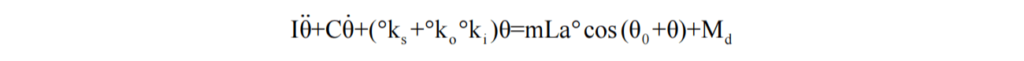
Linear kinematics model

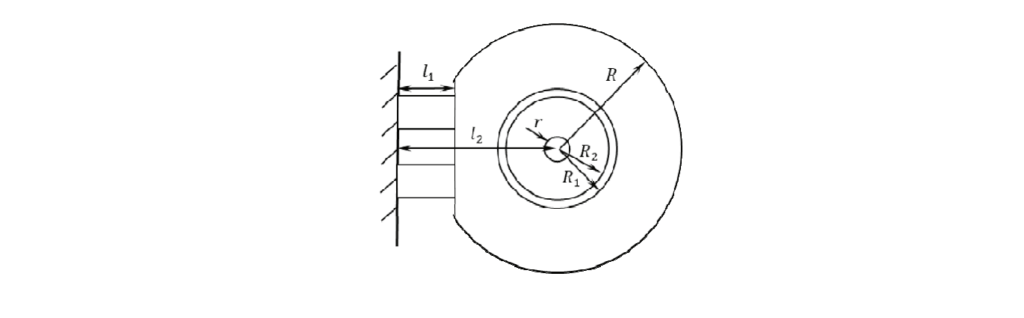
2.2 Low Coefficient of Thermal Expansion, High Stability Material Technology

2.2.1 Low Hydroxyl, Ultra-Pure Quartz Glass

Air bubbles, impurities, and hydroxyl groups in quartz glass can affect its mechanical properties such as strength, hardness, and elastic modulus, thereby reducing the performance of pendulum pieces and affecting the accuracy of quartz accelerometers. It is necessary to use high-performance materials with metal impurity content less than 1 ppm, hydroxyl group content less than 5 ppm, and optical non-uniformity within a φ100m diameter less than 2 ppm.

Due to the extremely low metal impurity and hydroxyl group content in such high-performance materials, and the most complete silicon-oxygen network structure in the glass structure, they possess characteristics such as high stability, high hardness, and high elastic modulus. Therefore, they are the preferred core components for high-precision strategic quartz flexible accelerometers.

2.2.2 Ultra-Low Coefficient of Thermal Expansion Alloy

The main cause of structural dimension instability is the change in component dimensions due to environmental temperature variations. The smaller the coefficient of thermal expansion of the component material, the smaller the dimensional changes caused by environmental temperature changes, resulting in better overall structural dimensional stability.

Upper and lower yokes and loops typically employ the low expansion alloy 4J36 (Fe-Ni36). By further adjusting and modifying the chemical composition of the material and applying ultra-pure melting, a class of alloy similar to 4J36 with an extremely low coefficient of thermal expansion is obtained. This lowers the average thermal expansion coefficient of the alloy in the full temperature range (-40°C to 70°C) to 0.55 ppm, significantly enhancing its compatibility with quartz glass materials.

2.2.3 Dual Low-Temperature Coefficient High-Stability Permanent Magnet Alloy

Permanent magnets provide the energy for the working air gap magnetic field, and the rational selection of permanent magnet materials is a key part of magnetic circuit design. The stability of accelerometer scale factor and temperature coefficient depends largely on the stability and temperature coefficient of the permanent magnet material's magnetic properties. The basic principle for selecting permanent magnet materials is to choose materials with high magnetic energy product, high residual magnetism, high coercivity, and low temperature coefficient.

New types of permanent magnet materials with low residual magnetism temperature coefficients and low coercivity temperature coefficients, while ensuring the residual magnetism temperature coefficient, also have coercivity temperature coefficients lower by an order of magnitude than traditional magnetic materials. This effectively reduces the magnetic field drift caused by fluctuations in coercivity, resulting in better temperature stability and time stability of the magnetic field, potentially ensuring long-term stable use of quartz accelerometers in variable temperature environments.

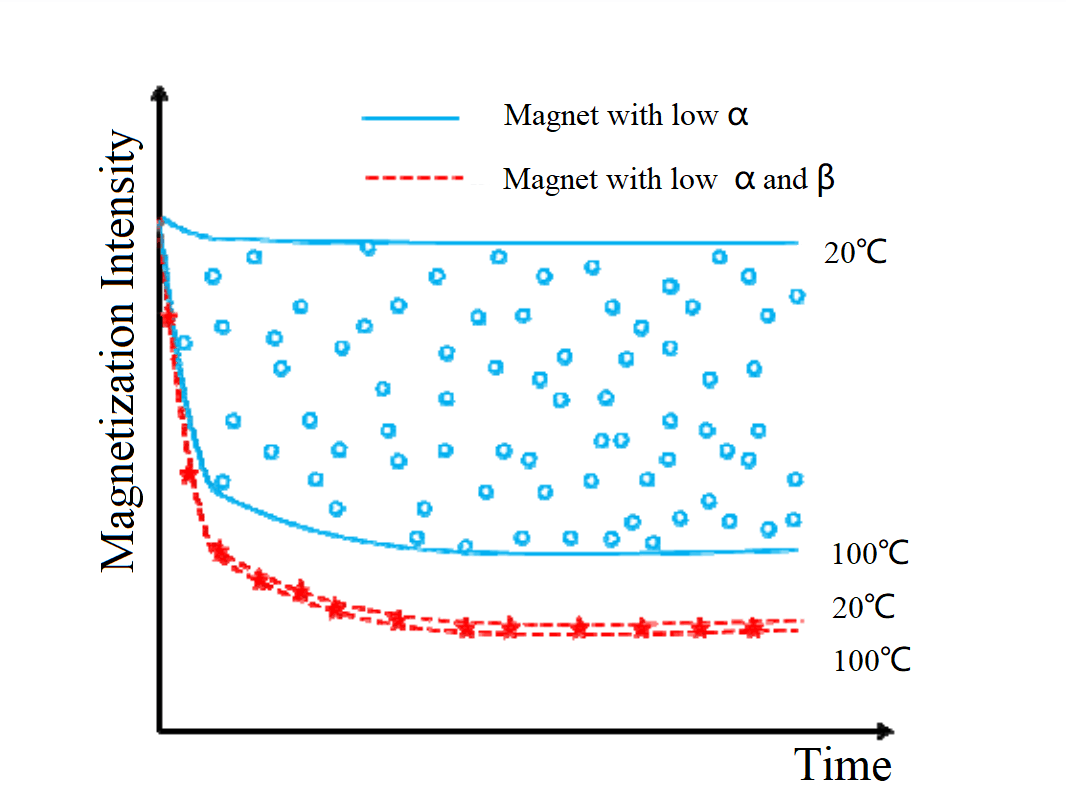
Fig.5 Magnetic attenuation diagram of traditional magnets with coefficient α and a new type of magnet with coefficient α and β

Note: α is low remanent temperature coefficient and β is low coercivity temperature coefficient

2.3 Low Stress Control Technology and High-Precision Machining and Assembly Technology

Since quartz flexure accelerometers are ultra-high-precision instruments, the machining level of components has a huge impact on product quality, and the level of geometric tolerance technology determines the performance of the product. In order to maintain the long-term stability and performance retention period of accelerometers, it is essential to focus on low-stress machining of components and low-stress assembly to achieve stress control and elimination accurately.

3.Nano-g Level High-Stability Accelerometer Evaluation System and Application Technology

According to the testing requirements of high-precision instruments, the stability of acceleration provided by the testing environment must far exceed the accuracy of the accelerometer itself. Developing a high-stability testing environment to meet the requirements of high-precision instrument testing is crucial. The adjustment and calibration of high-precision accelerometers must be based on a higher-precision testing environment, testing equipment, and more comprehensive test methods.

4.Conclusion

This article proposes measures to maintain the long-term stability of accelerometers based on the structural mechanism of sensors, theoretical mathematical models, and improvements in materials, high-precision machining technology, and high-accuracy testing environments.

It is worth noting that the ER-QA-03C quartz accelerometer exhibits outstanding performance, with a scale factor of 1.0 ± 0.2 mA/g. The zero offset repeatability of the 03C1 series is ≤15 μg, and the scale factor repeatability is ≤15 ppm. It has extremely wide applications in fields such as aerospace, aviation, navigation at sea and on land.